VaranasiでPuzzle 〜 ハノイの塔とそのバリエーション †


Varanasiには、4枚の異なる大きさのディスク×6色が入っています。これを使えばハノイの塔やそのバリエーションが遊べます。
ハノイの塔は、日本でもパズルファンや情報科学*1を学ぶ人には知られているパズルの名作古典です。一方で、Abstract Strategy Game Societyやゲームマーケットで、Varanasiを紹介する際、「ハノイの塔をご存知ですか?」と尋ねても、多くの人はご存知ではなく、近年の複雑なパズルや数独ほどには認知されていないようです。
ここでは、せっかくですので、1人完全情報ゲームであるパズルの名作と、そのバリエーションを紹介しましょう。
オリジナルのハノイの塔は、ディスクの中央に穴が空いていて、ボードに立てられた3本の支柱にディスクを差し込むようになっています。
Varanasiの駒とボードを使う場合には、支柱の代わりにボード上に描かれた7ヶ所の図案などを目印にディスクを配置すると良いでしょう。
 |
 |
 |
 |
 |
| 2ヶ所 | 1ヶ所 | 1ヶ所 | 1ヶ所 | 2ヶ所 |
ハノイの塔 †
History †
ハノイの塔のパズルは、フランス人の Édouard Lucas によって1883年に考案されました。
ハノイの塔のリーフレットに掲載されている話は、有名でWikipediaの日本語ページなど各所で紹介されています。
ハノイの塔は日本では、明治時代に参考文献/世界遊戯法大全で紹介されました。本書では、ハノイの塔に同梱されたリーフレットの話についても紹介しています。以下にその内容を、本文をできるだけ尊重して現代語にして紹介します。
英領インドのベナーレズ*2に大きい伽藍(がらん)があって、その丸天井は世界の中心と言う事であるが、これに、高さ1呎(フィート)半大きさ蜂の体ぐらいの3つの金剛石の針が立っている。この針の1つに、世界創造の時、神が置かれたそうで、64個の金の円板がはめてあり、1番下のが1番大きく、上になる程次第に小さい、これをブラマ*3の塔というて昼も夜も、僧侶はブラマ教に定めてある法則を守って、1つずつ他の釘に移しているが、これを移す時やはり小さい円板が、大きいのの下になるような事はせられないのである。かくてこの円板が神の初めにはめられたように、他の針に移された暁は、即ち世の終わりで、天地鳴動万物ことごとく散り失せるとの事であるが、さてこれをしとげるには何度円板を移し換えねばならないかというに、2&super{64};-1 即ち 18,446744,073709,551615回で、しかもこれ僧侶が1度も間違えない時の回数で、これでも幾百万年かかるか知れないのである。ちなみに云う河内(ハノイ)とは、仏領インドシナの首都の名である。
最期の1文は、リーフレットの翻訳ではないでしょう。文体や、各地が英領、仏領であることなど、時代の違いがよくわかって、とてもおもしろいと思いませんか。
ハノイの塔 基本ルール †
このパズルでは、目印となる地点(寺院, 象, 銅像)を3ヶ所使います、どの地点を使うか事前に決めておきましょう。
一種類の色を選んで、すべてのディスク(4個)をボード上の内1つの地点に図のように、小さいものが上になるように順に積み重ねて配置します。

挑戦者は、ディスクを1回に1枚ずつどれかの地点に移動させます。
小さな円盤の上に大きな円盤を乗せることはできません。
すべてのディスクをはじめに配置した地点と異なる地点に移動させられれば完成です。
最短手数は、何手になるでしょうか。
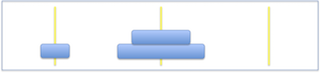
3ディスクでの解答例
 |
 |
 |
 |
| 初期配置 | Step1 | Step2 | Step3 |
 |
 |
 |
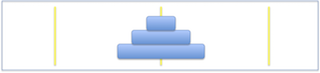 |
| Step4 | Step5 | Step6 | 完成! |
2色のハノイの塔 †
2色のディスクを選び、図のように色が交互になるように配置します。

使う地点は基本ルールと同様3地点。
基本ルールと異なる移動ルールは、同じ大きさのディスクも上にのせることができることです。
下図のようにディスクを色分けできたら完成です。
 |
 |
| 簡単ゴール(一番下のディスクが元の位置と同じ) | 困難ゴール(一番下のディスクが元の位置と異なるポイントに移動) |
このパズルは、図のように簡単ゴールと困難ゴールの2つのパズルを遊んでみましょう。
磁石ディスクのハノイの塔 †
移動できる地点は、基本ルールと同様3地点。 青と赤のディスクを図のように配置する。このパズルでは、青(S極)と赤(N極)で、青赤のディスクが1つのもの(くっついている)として遊びます。

基本ルールと同様にディスク(青赤セットで)を移動します。
移動するたびに、ディスクの上下(青赤)をひっくり返します。 同じ極どうしは反発してしまうので、青-青,
赤-赤となるようには配置できません。
ゴールは基本ルールと同じです。
基本ルールの最小手数とくらべて、このルールの最小手数はどうでしょう。
循環ハノイの塔 †
基本ルールと同様に3地点と1つの塔を配置してはじめます。
ディスクは、移動先が必ず A地点->B地点->C地点->A地点
となる順番にしか移動できません。
あとは、基本ルールと同じです。
基本ルールの最小手数とくらべて、このルールの最小手数はどうでしょう。
4地点以上を移動できるハノイの塔 †
4地点以上を使ってパズルを解いてみましょう。
基本ルールの最小手とくらべて、短い手順で解けましたか。
複数の塔のハノイの塔 †
複数の塔(色)を使ったパズル*4

配置した塔、すべてをはじめの位置と異なる場所に移動させます。
a. 同じ大きさのディスクは重ねられないルール †
はじめに設置する塔の地点数+2つの空き地点を使って、すべての塔を移動させます。
2つの塔であれば、4地点あれば完成できるかな!?
b. 同じ大きさのディスクは重ねて良いルール (2色の拡張版) †
はじめに配置する塔の地点数+1地点あればできる??