アブストラクトゲームと数学

Amazonでボードゲームを探す

このコーナーでは、アブストラクトゲームと数学の関係や、ゲームの設計に潜む数理科学用語などを紹介します。

数学コラムのコーナー †

↑

Fano Plane †

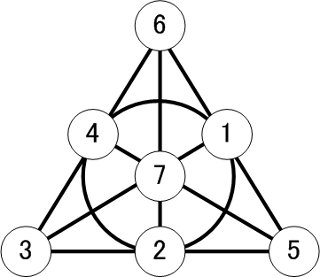
FIRE and ICEは、Fano Planeをデザインの基本にしたゲームです。

Fano Planeとは位数2のFinite Plane(有限平面)もしくは射影平面(Projective Plane)のことです。(日本語では射影平面という呼び方の方が一般的かもしれません。)

位数 q の射影平面とは、次の条件を満たす図形です。

q&super{2}; + q + 1 個の点からなり、

どの直線も q + 1 点を通る

どの２点も、ただ１つの直線に乗る

Fano Planeは、q=2の時の図形で、図のような形になります。いずれの点や線も、上記の条件を満たしていることが確認できます。 (この平面上では、頂点{1,2,4}の内接円も直線とみなすことをご理解ください。)

別の言い方をすれば、頂点の集合{1,2,3,4,5,6,7}における、Fano Planeの端は、 {1,2,4}, {2,3,5}, {3,4,6}, {4,5,7}, {5,6,1}, {6,7,2}, {7,1,3} と言えます。これらの端は、三要素{1,2,4}にそれぞれ、7を法として1ずつ加えることで生成できます。生成規則によって作られた三要素は、他のいずれの二つの要素とも異なり、いずれの順序においても、すべての対応する要素が7を法として異なる要素を持っています。

Fano330-R-Morrisは、まさにこの図形をゲームボードとしたアブストラクトゲームです。
FIRE and ICEでは、この7種類の端の組み合わせが、島の征服条件であり、どうようのパターンで島をつなげた場合に勝利条件になっています。

↑

ゲームの解決 †

論理的には、アブストラクトゲームとコンピューター2で言及したように、Mini-Max法によって、(主に二人で対戦する)アブストラクトゲームは、どちらのプレーヤーが勝つか、引き分けるかといった解を得ることができます。しかし、当館に掲載してあるようなほとんどの単純でないゲームは、ゲームの探索空間が広く、現実時間内に、すべての場合を計算し尽すことが困難です。しかし、ゲームの顛末はどうなるのかについて、数学的な考察によって探索空間を狭める工夫に加えて、膨大なコンピューター時間を費やすなどによって、いくつかのゲームが解決されています。

ゲームの研究において、解決のレベルをしめすために使われる用語がありますので簡単に解説しておきます。Solved Gameについて、英語版WikiPediaでは充実した情報が掲載されていますが、日本語の情報が見当たりませんので、ここでは、英語版WikiPediaに書かれている内容を中心に紹介します。

Ultra-weak: 極弱く(解決)
完全な手をお互いが指した場合、「先手必勝か、後手必勝か、または引き分けになるか、ゲームの開始時点からわかっている」ことが証明できている。完全な手を決定しえないような、構造的でない証明によるものでも構わない。
例えば、Hexは、NashによってUrtra-weakに解決されたゲームです。

Weak: 弱く(解決)
普通「解決されている」状態というと、この「Weakに解決されている」状態を指す。ゲーム開始時から、起こりうるすべての合法手に対して、勝利、引き分け、負けになるアルゴリズムが提示されている。
Connect 4, 立体四目並べ／ Qubic他、多くの解決されたとされているゲームは、Weakに解決されたゲームです。

Strong: 強く(解決)
(どちらか、または両方のプレイヤーがさし間違いのミスを犯した後も含む)すべての局面において、完全な指手を生成できるアルゴリズムを提示することができる。
探索空間の狭いTic-tac-toeや、論理的な必勝手順が示されているnimは、Strongに解決されたゲームです。

↑

Perfect play / 完全な手 ... 最善手 †

完全な手とは、相手の手に関わらず、プレイヤーを最善の結果をもたらす戦略/選択のことです。2Playerのアブストラクトゲームは、ゲームの終了*1時点では、必ず、どちらかのプレーヤーが勝っているか、引き分けになっていますので、その状態から帰納的に完全な手=意図的に自分に不利な手を選択しないような手を選択して、途中局面までさかのぼり、途中の局面についても評価を与えることができます。同じ結果になるような複数の選択肢がある場合には、自分に有利な結果なら最短でそこにたどり着く、自分に不利な結果になるなら最長の手数を費やす、手を完全な手と限定することがあります。

↑

フラクタル †

The Ring Worldのボードのフラクタルアニメーション
Flash廃止によりサービス終了

フラクタル図形とは、自己相似性な性質を持つ図形のことを言います。自己相似な図形とは、図を拡大してみると、内部に同じ形の図が無限に繰り返される構造を持つ図形です。

代表的なフラクタル図形には、コッホ曲線、カントール集合、マンデルブロー集合、ペアノ曲線、シェルピンスキーのギャスケットなどがあります。それぞれ、考案者に由来する名前がつけられています。

↑

フラクタル次元 †

複雑な、フラクタル図形を定量的にあつかうために、従来の幾何次元を見直した、フラクタル次元があります。フラクタル次元は、従来の幾何図形次元(点=0次元, 線=1次元, 面=2次元, 立体=3次元)とコンパチブルな上位の概念です。

対象となる図形をn等分すると、分割された図形がm個含まれているとき、フラクタル次元を、次のように定義します。
log&subsc{n};(m)
この考えに基づいて、
線分は2等分すると2個の同じ形の図形になるので、log&subsc{2};(2)=1
正方形は各辺を2等分すれば4個の正方形になるので、log&subsc{2};(4)=2
というように、計算できます。

ただし、フラクタル図形と呼ばれる図形は、フラクタル次元が整数にはならない性質があります。

右図The Ring Worldのボードも、このフラクタル次元が非整数になる性質を満たしています。この図形については、The Ring Worldのボードについてにて詳しく考察します。

↑

オートマトン †

The Life Game
Flash廃止により、サービス終了

オートマトン(Automaton)は、自動人形を表す言葉です。アブストラクトゲームとオートマトンの関係は、History of Chessで紹介する、 18世紀にいくつか登場したChessをプレーする人形があります。

近年、情報科学の発展に伴い、オートマトンは、プログラム(形式)言語を解釈するシステムなどのシステムの内部状態を保持して自動で動作する複雑(に見える)なシステムの特徴を表すために用いられています。

英国の数学者Conwayによって考案されたライフゲームは、二次元平面をグリッドに分割し、それぞれのグリッドの周囲の状態で遷移するセル・オートマトンの代表です。

グリッドの状態は、onとoffの二種類で、以下のルールに従って、次世代の状態に遷移します。グリッドがonの場合、周囲にonのグリッドの数が

1個以下　過疎により死滅します
2,3個次の世代に生き残ります
4以上過密により死滅します

グリッドがoffの場合、3個のonグリッドに囲まれた場所は、次の世代でonになります。

方眼用紙一枚に、一世代ずつの状態を描いて、複雑に状態が移り変わる様子を確認することができます。コンピューターを使えば、より手軽にライフゲームを体験できるので、FortranやBasicなどの言語で、ライフゲームをプログラミングした方も多いのではないでしょうか。館長と富永先生の共著awkでプログラミングにも、awkで記述したライフゲームが掲載してあります。

ライフゲームのアイディアは、あまりに多くの人を魅了し、ライフゲイムの宇宙をはじめとする書籍や記事が発表され、後にたくさんの派生オートマトンが生まれました。

ライフゲームは、対戦を目的としたゲームではありませんが、このアイディアを対戦型のゲームに発展させるアイディアも複数見つけることができます。

当館のオリジナルゲーム、The Ring Worldにも、単純なオートマトンの仕組みが組み込まれています。

↑

オイラー数 †

オイラー数は、整数列を示す数と区別するため、オイラー標数ともよばれる、図形の特徴を表す数です。高校生ぐらいまでの数学では
多面体の頂点数 V, 辺の数 E, 面の数 F とすると、オイラー数Χは、

Χ = V - E + F

と勉強されたのではないでしょうか。凸多面体ならばこれは常に2になります。

↑

Nimber / グランディー数 †

↑