nim

HISTORY †

nimは、古くから(どれくらい前からかはよくわかりません)遊ばれている石取りゲームです。おそらく中国が発祥だろうと考えられていますが、確かではありません。

類似のゲームも古来から、数多く存在しています。

マーチンガードナーの数学ゲームによると、1901年に、米国ハーバード大学の Charles L. Bouton がゲームの分析を発表したときに、このゲームをnimと命名したのだそうです。この名は、Boutonが英語の古語のnim=取るの意味か、ドイツ語のnimmから取ったのではないかとガードナーは推察しています。*1

↑

DESCRIPTION †

↑

SETUP †

任意の数の石を、任意の列並べます。

↑

MOVE †

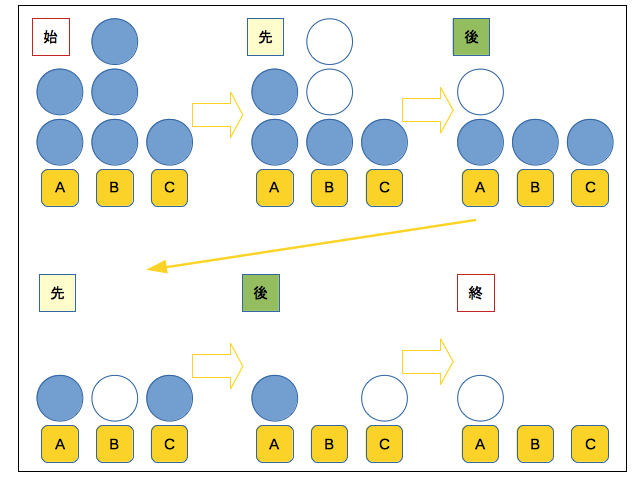
任意の一つの列から、一つ以上好きなだけ石をとります。

パスはできません。

↑

GOAL †

二つのルールがあります。

最後の石を取ったプレーヤーが勝ち (正型)
最後の石を取ったプレーヤーが負け (逆型)

↑

STRATEGY †

参考文献/石とりゲームの数理, 参考文献/ゲームと競技の数学遊びのサイエンス, 参考文献/ゲームにひそむ数理などに詳しい研究が掲載されています。

ここでは、簡単に戦略を紹介しましょう。正型のnimと逆型のnimで、戦略上の難しさが異なります。

↑

正型 †

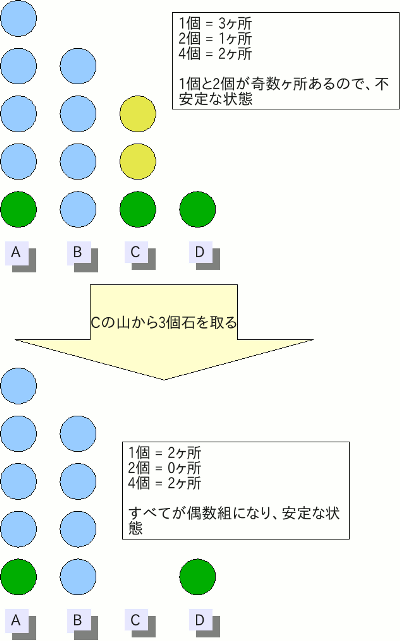
正型のnimでの必勝手順は、それぞれの山を二のべき乗個にべき数重ならないように分類し、すべての山について同じべき数を持つものの合計が、いずれも偶数個になるように石を取っていきます。この状態を安定な状態と呼びます。

自分の手番で安定状態を作れれば、勝ちのパターンに入っているわけです。

↑

逆型 †

とすると、逆型のnimはその反対の戦略をとればいいかと考えますが、実はそれほど簡単ではありません。正型のnimの勝つ状態(手番で安定な状態にした)が負ける状態。負ける状態が勝つ状態に、必ずしも単純にはならないのです。

もし、どの山も一つの石しか持たなければ、正型の勝ち状態が負けの状態になります。しかし、いずれかの山に二つ以上の石がある場合は、状態が逆転します。

そこで、逆型のnimに勝つための戦略を立てると

いずれかの山に二つ以上の石が残っているうちは、正型の時と同じ戦略でゲームを進め
すべての山が一つの石しかない状態になると、相手の手番に奇数個の山が残るように石を取ります *2

☆☆ ☆☆ ☆☆

戦略の詳細は、nimをプレーするコンピューター・プログラムで記載します。

↑

NOTE †

nimのルールは単純ですが、奥深いゲームです。

数学的には、戦略と理論が完全に整理されていて、対等な二人ゼロ和完全情報で必ず決着のつく*3ゲームの典型としてあつかわれる重要なゲームでもあります。必ず決着のつく対等な二人ゼロ和完全情報ゲームに分類されるものは、すべてnimと数学的に同等なことが確かめられています。この種のゲームをImpartial Gameと呼びます。

↑